*해당 게시글은 2022.06.16 파이썬 금융코드 작성본을 업로드한 게시글입니다.
[평균, 분산, 표준편차]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
nums = [1,2,3,4,5]
#평균
avg = sum(nums)/len(nums)
#각숫자 - 평균의 제곱
sumsquare = sum((n-avg)**2 for n in nums)
#분산
var = sumsquare/(len(nums)-1)
#표준편차
import math
sd = math.sqrt(var)
print(sd)
|
cs |
[matplotlib 이용한 정규분포]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
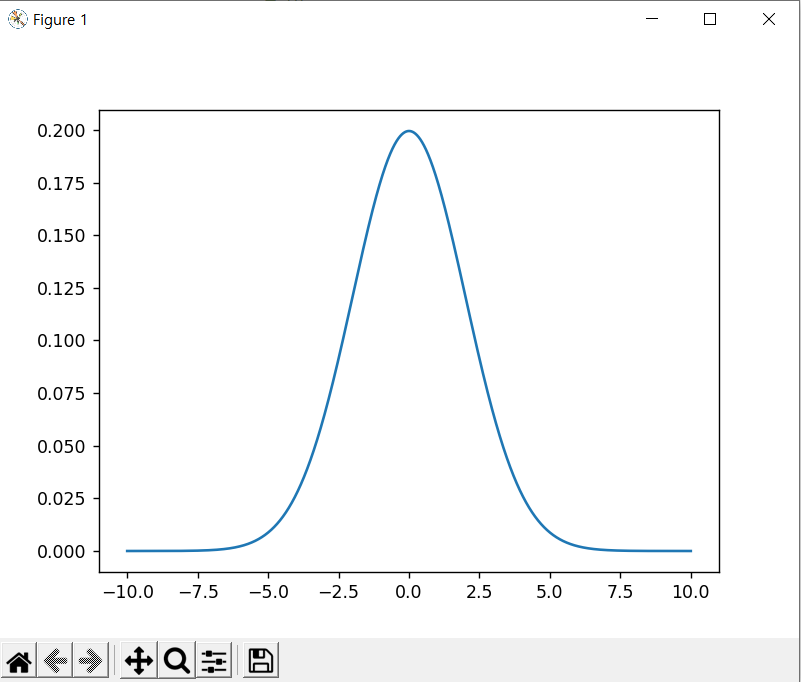
# matplotlib을 이용한 -10 ~ 10 사이에서 평균이 0, 표준편차가 2인 정규분포
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# x축은 -10에서 10사이에서 0.001 간격으로 설정
x_axis = np.arange(-10,10,0.001)
# 평균 = 0, 표준편차 =2 인 정규분포
plt.plot(x_axis, norm.pdf(x_axis,0,2))
plt.show()
|
cs |
[numpy를 이용한 표준편차, 공분산, 상관계수 구하기]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#공분산과 상관계수
#상관계수는 공분산과 두 변수의 표준편차곱 간의 비율이다. 그렇기 -1~1만 나온다.
import numpy as np
x=np.array[41,43,38,37]
y=np.array[61,63,56,55]
#표준편차 구하기
x_std = np.std(x)
y_std = np.std(y)
#공분산 구하기
cov = np.cov(x,y)[0][1]
#상관계수 구하기
corr = np.corrcoef(x,y)[0,1]
print(x_std)
print(y_std)
print(cov)
print(corr)
|
cs |
'투자 > 퀀트' 카테고리의 다른 글
| 퀀트, 파이썬 / 삼성전자와 필라델피아 반도체지수의 상관관계 구하기 / numpy, pandas 사용 (0) | 2022.06.17 |
|---|---|
| 퀀트, 파이썬 / 기초코드 저장소(3) / numpy 이용해서 MMD 구해보기 (0) | 2022.06.16 |
| 퀀트, 파이썬 / 기초코드 저장소(1) / Numpy -financial, numpy (npv, irr, 기하평균, 산술평균, 기댓값, 가중평균) (0) | 2022.06.16 |
| 파이썬, 구글 코랩 / 퀀들(Quandl)로 금 가격 데이터 추출 (0) | 2021.08.02 |
| 파이썬, 구글 코랩 / 야후 파이낸스로 주식 수익률 계산 (0) | 2021.07.12 |




댓글